A Critical Review of Modular Bayesian Frameworks for Real-Time Uncertainty Quantification in Autonomous Systems
Autonomous systems operating in contested environments require real-time uncertainty quantification under adversarial interference and sensor degradation, yet existing approaches struggle to balance computational tractability with probabilistic rigour. This review aims to sketch whether modular Bayesian frameworks can reconcile this tension by decomposing complex digital twins into linked components that enable efficient computation whilst maintaining principled uncertainty propagation. Through thematic synthesis of foundational works and recent contributions spanning probabilistic graphical models, multi-fidelity modelling, and Bayesian verification methods, the review identifies patterns across four dimensions: modular decomposition strategies, information-passing mechanisms, computational efficiency approaches, and uncertainty quantification methods. The synthesis reveals a critical limitation: all current methodologies rely on static architectures with fixed module dependencies and predetermined information-passing protocols specified at design time. When operational regimes shift, precisely when accurate uncertainty quantification is most critical, these fixed structures propagate information along channels that no longer reflect actual statistical dependencies. Three interconnected research directions emerge: adaptive graphical model structures that dynamically reconfigure based on observed data, context-aware information-passing protocols that balance sparse efficiency against dense accuracy, and dynamic approximation strategies that adjust fidelity based on computational resources and decision urgency. These capabilities are essential for autonomous operations in denied, degraded, and operationally limited environments, representing a fundamental shift from human-reconfigured systems to truly autonomous uncertainty quantification across operational transitions.
Introduction: The Challenge of Real-Time UQ in Modular Systems
The deployment of autonomous systems into contested and high-variability settings represents one of the most technologically demanding applications of modern Sensing, Processing, and Artificial Intelligence (AI) for the Defence and Security domain. These systems must make mission-critical decisions under severe time constraints, incomplete information, adversarial interference, and evolving operational contexts (Kapteyn et al., 2021). Traditional approaches to system modelling and control, such as monolithic physics-based simulations, prove inadequate for this challenge, as they are computationally prohibitive for real-time deployment and frequently offer limited transparency into subsystem interactions (Ming et al., 2023).
Digital twin technology has emerged as a promising paradigm, offering virtual representations of real-world processes, environments, or objects that must predict the associated real-world entity's response to a stimulus, and remain tied to it to a known tolerance and without statistical bias (Defence Science and Technology Laboratory, 2022). The autonomous deployment of digital twins remains constrained by the fundamental tension between achieving real-time computational tractability and rigorously quantifying the pervasive uncertainty generated by contested, mission-critical environments. Modular decomposition offers a potential resolution to this tension. By partitioning complex digital twins into linked components that correspond to engineering subsystems (propulsion, navigation, communication, sensing, and so forth—modular frameworks promise to achieve computational tractability through divide-and-conquer strategies while maintaining transparency and interpretability (Wilson et al., 2018; Volodina et al., 2022). The critical challenge lies in ensuring that this decomposition does not compromise the propagation of uncertainty across module boundaries.
Recent work has begun to establish theoretical foundations for probabilistic digital twins. Kapteyn et al. (2021) propose a unified mathematical framework based on dynamic decision networks, synthesising Dynamic Data-Driven Application Systems (DDDAS) paradigms (Darema, 2004), partially observable Markov decision processes (Russell & Norvig, 2002), and probabilistic graphical model theory (Koller & Friedman, 2009) into a coherent approach for cyber-physical systems like an unmanned aerial vehicle (UAV). Their framework introduces a six-quantity abstraction that enables modular representation while preserving principled uncertainty quantification. Zhao et al. (2024) extend this foundation to verification of autonomous robots, demonstrating how Bayesian learning can provide provable safety guarantees. Chen et al. (2025) address real-time constraints through uncertainty-aware model predictive control using deep learning for quantile estimation.
Despite these advances, fundamental questions remain unresolved. Current frameworks assume static module dependencies that cannot adapt to changing operational regimes. Information passing mechanisms between modules often rely on simplifying independence assumptions that may not hold under adversarial or fault conditions. Computational efficiency techniques (e.g., sparse approximations, variational inference, multi-fidelity modelling) introduce approximation errors whose impact on end-to-end uncertainty estimates is poorly understood. This review addresses the central research question: How can modular Bayesian frameworks enable computationally efficient, real-time uncertainty quantification when integrating multiple information sources in complex systems?
Methodology
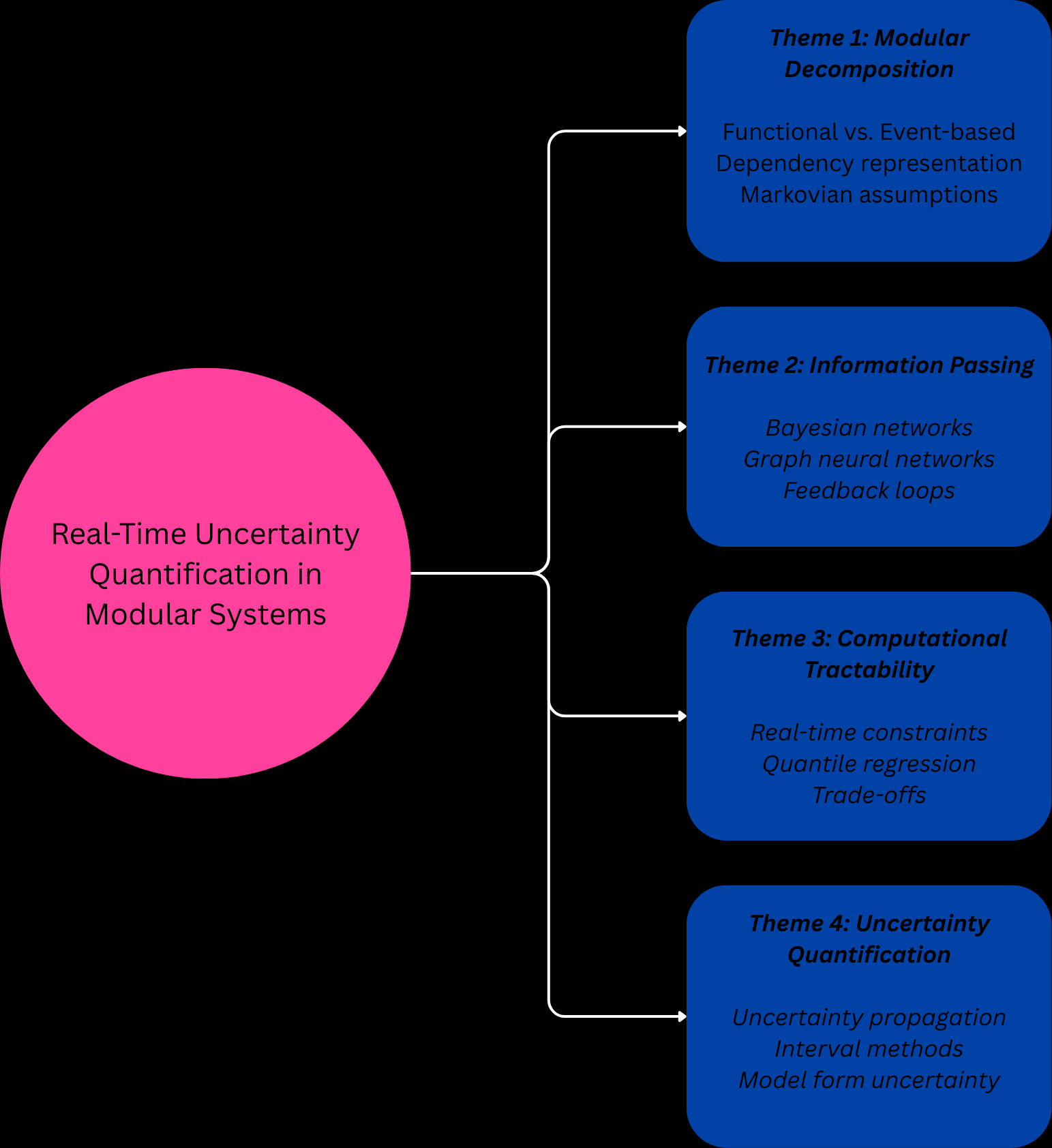
Figure 1: Analytical framework structuring the review synthesis. Each theme addresses a distinct methodological challenge in modular Bayesian frameworks: decomposition strategy (Theme 1), information flow (Theme 2), computational feasibility (Theme 3), and uncertainty management (Theme 4).
The review employs thematic synthesis to identify patterns, tensions, and gaps across the literature. Primary papers were analysed along four dimensions (Figure 1): modular decomposition strategies, information-passing mechanisms, computational efficiency approaches, and uncertainty quantification methods. For each theme, the synthesis identifies convergent findings, contradictory results, and unresolved challenges. The gap analysis then synthesises these themes to articulate fundamental research questions that remain unaddressed by current methodologies, facilitating the identification of cross-cutting issues that span multiple methodological areas and revealing opportunities for novel integrative approaches.
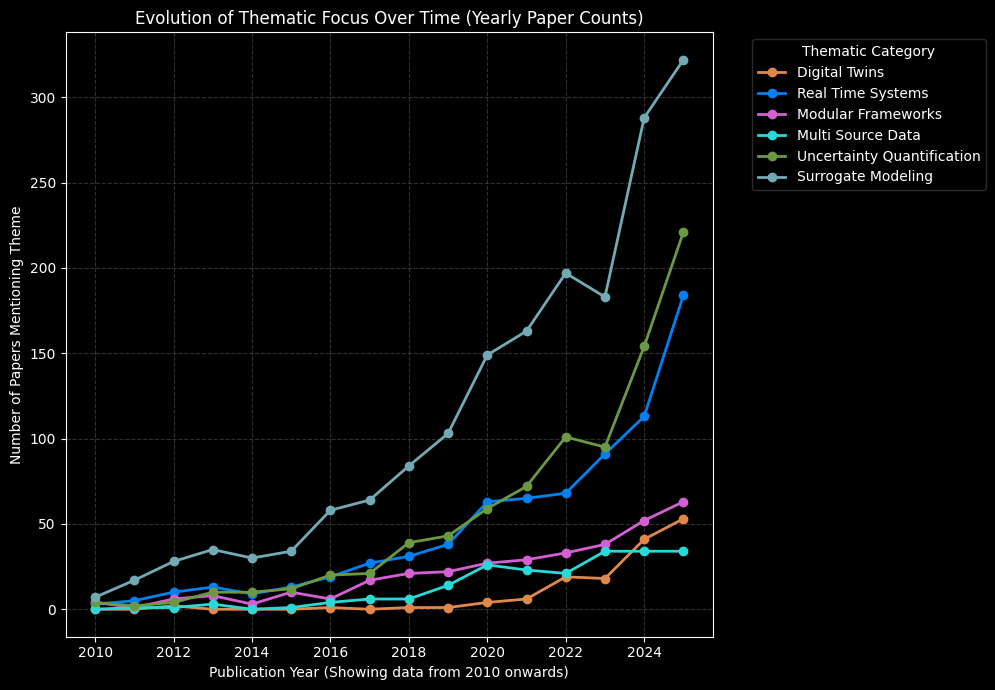
Figure 2: Temporal Evolution of Thematic Focus (2010–2025). Yearly publication count for the six thematic criteria, illustrating the relative emergence and growth rate of key methodological and application concepts within the corpus.
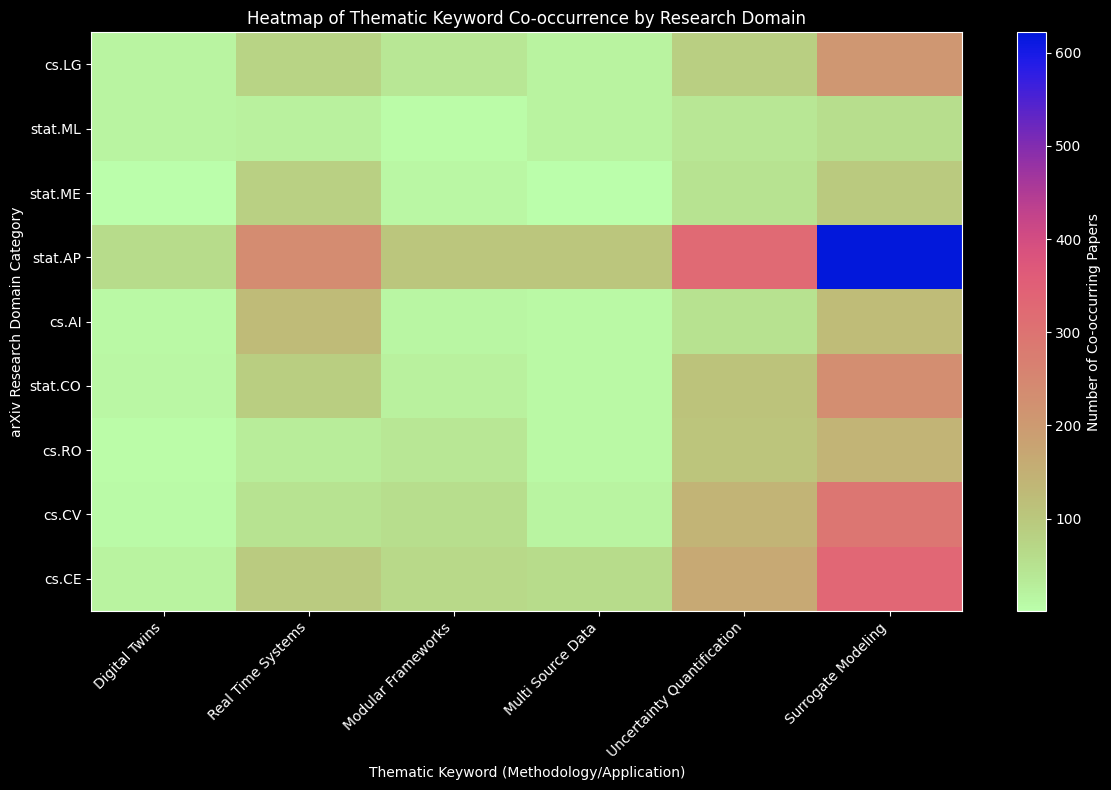
Figure 3: Domain-Theme Co-occurrence Heatmap. Intensity of co-occurrence between the top 10 arXiv research categories (y-axis) and the six thematic criteria (x-axis), revealing the disciplinary clustering of research focus.
To contextualize the methodological landscape, a programmatic analysis of 1,247 papers from arXiv (2010-2025) was conducted using structured keyword queries across six thematic criteria. Figure 2 reveals three critical temporal patterns: the explosive growth of Surrogate Modelling papers (300+ annually by 2025) far outpaces Digital Twins (<60 annually), suggesting the field prioritizes computational approximation over system-level integration; the delayed emergence of Digital Twins literature post-2020 confirms this remains a nascent application domain; and the modest growth in Modular Frameworks indicates decomposition strategies have not achieved mainstream adoption despite their theoretical appeal. Figure 3 exposes disciplinary fragmentation: Statistics (stat.AP) and Machine Learning (cs.LG) communities concentrate overwhelmingly on Surrogate Modeling, while Real-Time Systems and Modular Frameworks show weak representation across all domains. This fragmentation explains the gap identified in Section 4, no single community has integrated modularity, real-time constraints, and uncertainty quantification within a unified framework. The convergence required for practical digital twin deployment remains absent from current research trajectories.
The synthesis draws on a curated set of primary papers identified through systematic searches and citation tracing. Selection prioritised work addressing modularity, Bayesian uncertainty propagation, computational efficiency, and applications in digital twins or autonomous systems. The final corpus spans three broad categories: survey papers establishing the state of the field, foundational works providing core theoretical tools, and recent contributions showcasing emerging methods in probabilistic digital twins, uncertainty-aware autonomy, and multi-fidelity modelling.
Critical Synthesis: Modular Architectures and Uncertainty Propagation
Probabilistic Graphical Models for Modular Digital Twins
The foundational challenge in modular digital twin architectures involves maintaining probabilistic coherence across decomposed components while avoiding the computational intractability of joint inference over all system variables. Probabilistic graphical models offer a mathematically principled framework for addressing this challenge through factorized representations of joint distributions that exploit conditional independence structure (Koller & Friedman, 2009).
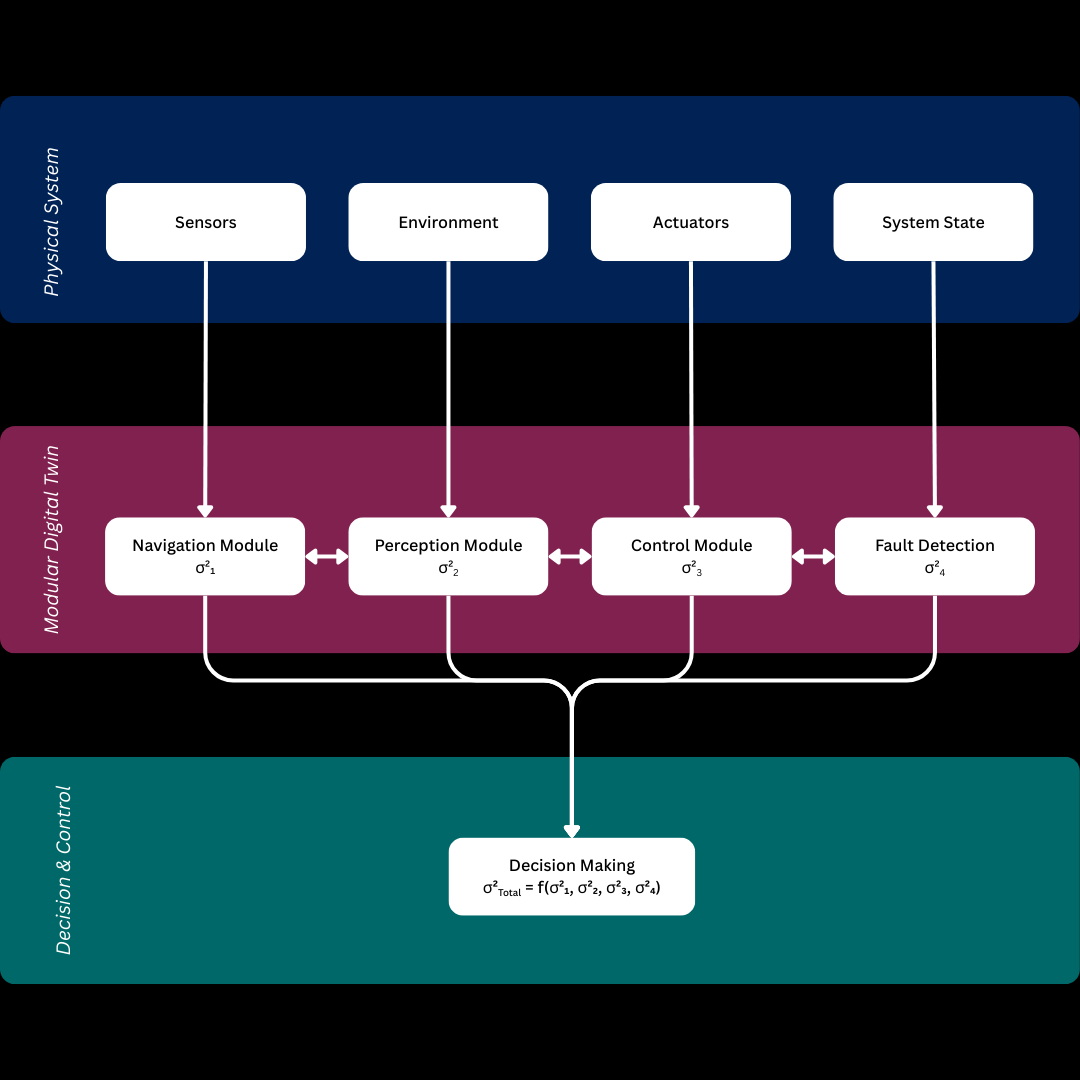
Figure 4: Modular Digital Twin Architecture illustrating information flow and the propagation of local uncertainty (σi2) through conditional dependencies to a total uncertainty (σtotal2) that informs the decision-making process (Adapted from Kapteyn et al., 2021).
Kapteyn et al. (2021) provide the most comprehensive treatment of this problem for digital twins, proposing a unified framework based on dynamic decision networks. Their six-quantity abstraction (i.e., comprising design parameters, system states, sensor data, model predictions, decisions, and outcomes) enables modular representation through careful specification of conditional dependencies. This abstraction extends linked emulator frameworks previously developed for multi-stage engineering systems (Kyzyurova et al., 2018; Ming & Guillas, 2021), but introduces explicit treatment of decision-making and dynamic evolution essential for autonomous systems. The framework demonstrates how factorised joint distributions preserve end-to-end uncertainty quantification while enabling computational tractability through local inference operations (Figure 4). Figure 4 illustrates this hierarchical decomposition, showing how sensor data flows from the physical system through modular digital twin components (Navigation, Perception, Control, and Fault Detection modules), with each module maintaining local uncertainty estimates (σ²₁ through σ²₄) that aggregate into a total uncertainty measure (σ²total) for decision-making.
However, this elegant mathematical framework, as depicted in Figure 4, rests on a critical assumption: Markovian dependencies between system components. The sequential information flow shown between modules (Navigation → Perception → Control → Fault Detection) assumes that, module outputs at time t depend only on module inputs at t and states at t-1 excludes long-range temporal dependencies and spatial correlations that may arise from slowly-varying environmental factors, memory effects in materials, or correlated failure modes. Sauer et al. (2022) demonstrate that deep Gaussian processes can capture such dependencies through hierarchical latent variable structures, but at substantial computational cost that may preclude real-time deployment. The computational complexity scales poorly with the depth of the hierarchy and the dimensionality of latent variables.
Ming et al. (2023) propose stochastic imputation as a potential middle ground between full Bayesian treatment and crude independence assumptions. Their approach achieves analytically tractable predictions through carefully structured linked Gaussian process formulations while avoiding the computational burden of fully Bayesian inference over deep hierarchies. The key insight involves treating intermediate quantities as latent variables with analytically marginalizable distributions, enabling efficient information propagation through the module graph. However, this approach requires careful specification of which dependencies to model explicitly versus marginalize, and provides limited guidance for making these decisions in novel application domains.
The choice of decomposition strategy itself significantly impacts both computational tractability and the validity of independence assumptions. Kapteyn et al. (2021) employ functional decomposition, partitioning systems according to engineering subsystems (propulsion, navigation, etc.). This aligns naturally with engineering practice and domain expertise, but may not correspond to the statistical dependencies that actually govern system behaviour. Zhao et al. (2024) advocate an alternative: event-based modularity that separates singular events (failures, attacks, extreme conditions) from regular operational behaviour, employing specialized estimators for each regime. This approach connects to reliability engineering traditions of hierarchical Bayesian models for rare events (Bishop et al., 2011; Strigini & Povyakalo, 2013) and interval-based reasoning for systems with limited training data on failure modes (Češka et al., 2016). The event-based decomposition may better capture the statistical structure of autonomous systems operating in contested environments, where adversarial actions and fault conditions constitute distinct probabilistic regimes.
Bayesian Network Architectures for Information Passing
Given a modular decomposition and associated dependency structure, the second critical challenge involves efficient propagation of probabilistic information between modules during inference. The computational tractability of this information passing determines whether real-time deployment is feasible.
Multi-fidelity modeling frameworks provide important insights into efficient information passing across hierarchically structured components. Zhang & Alemazkoor (2024) demonstrate how recursive multi-fidelity approaches, building on Kennedy & O'Hagan's (2000) foundational autoregressive formulation, enable decoupled training of components at different levels of a hierarchy. However, the autoregressive structure imposes strong constraints on the dependency patterns that can be represented efficiently. Specifically, it requires a linear ordering of modules such that each module's output depends only on inputs from modules earlier in the ordering. In the defence AI sector, digital twins often involve bidirectional (e.g., propulsion affects navigation, which in turn commands propulsion) or cyclic dependencies (e.g., sensing informs decision-making, which triggers communication, which then guides sensing). These complex, simultaneous feedback loops violate the strict ordering constraint of autoregressive frameworks. Representing such dynamics, ends up, requiring computationally expensive approximations, such as breaking cycles with delayed feedback or using iterative message-passing schemes that may not guarantee real-time convergence.
Graph neural networks (GNNs) offer a promising alternative that naturally accommodates arbitrary dependency graphs without linear ordering constraints. Taghizadeh et al. (2024) demonstrate that GNNs possess topology-aware inductive biases well-suited to multi-fidelity and multi-physics modelling, with message-passing paradigms that align naturally with probabilistic inference in graphical models. However, standard GNN architectures produce point predictions without principled uncertainty quantification, limiting their immediate applicability to digital twin frameworks requiring rigorous uncertainty propagation.
Computational Tractability and Real-Time Constraints
The third critical theme concerns computational efficiency. Even with optimal modular decomposition and information-passing architectures, achieving real-time performance for complex systems requires fundamental trade-offs between computational cost and the fidelity of uncertainty quantification.
Chen et al. (2025) confronts these trade-offs directly in the context of uncertainty-aware model predictive control for digital twins. Their approach employs deep learning for quantile regression, building on temporal convolutional architectures (Das et al., 2023) and multi-horizon forecasting methods (Fan et al., 2020) to achieve solving times of 0.1793 seconds (arguably, fast enough for certain control applications). However, this computational efficiency comes at the cost of sacrificing theoretical guarantees. Specifically, quantile regression provides empirical uncertainty intervals without the mathematical foundations of tube-based robust model predictive control (Mayne et al., 2000; Rawlings & Mayne, 2009), which offers provable recursive feasibility and stability guarantees. The learned quantile estimates may fail to generalise to novel operating conditions not represented in training data, precisely the contested environments where uncertainty quantification is most critical.
Uncertainty Quantification in Modular Architectures
The fourth theme concerns the specific challenges that modularity introduces for uncertainty quantification. While decomposition offers computational benefits, it complicates the propagation and aggregation of uncertainties across module boundaries.
Zhao et al. (2024) provide important insights through their work on Bayesian verification of autonomous robots. Their Bayesian Interval Probability Propagation (BIPP) and Interval-based Posterior State Probability (IPSP) estimators propagate bounded intervals rather than full probability distributions, extending conservative Bayesian inference frameworks (Walter & Augustin, 2009; Walter et al., 2017) to real-time robotic systems. These interval methods integrate naturally with probabilistic model checking tools like PRISM-PSY (Češka et al., 2016), enabling formal verification of safety properties. The key advantage lies in computational efficiency: interval arithmetic avoids the cost of Monte Carlo sampling or analytical integration, while interval bounds provide conservative certificates that guarantee coverage of true probabilities. However, interval methods suffer from pessimism: worst-case bounds over all possible values within input intervals can become excessively conservative after propagation through many modules, especially when correlations between module errors are neglected. The conservatism grows with system complexity, potentially leading to overly cautious decisions that sacrifice operational capability for theoretical safety margins that exceed actual risks. Balancing conservatism against operational effectiveness remains an art rather than a science.
Moreover, all reviewed uncertainty quantification methods implicitly assume that model structure is correctly specified, and that uncertainties arise only from parameter values, initial conditions, and stochastic inputs. Model form uncertainty, arising from simplifying assumptions, neglected physics, and discretization errors, has received substantial attention in the broader UQ literature (Kennedy & O'Hagan, 2001; Brynjarsdóttir & O'Hagan, 2014), but its systematic treatment within modular digital twin frameworks remains limited. For autonomous systems operating beyond their training envelope, model form uncertainty may dominate other sources. Modular frameworks could potentially enable more systematic treatment of model form uncertainty by representing competing model hypotheses as alternative modules and performing Bayesian model averaging, but this possibility remains largely unexplored.
Gap Analysis: The Need for Adaptive Modular Architectures
The critical synthesis across these four themes reveals a fundamental limitation shared by current methodologies: static modular architectures that cannot adapt to changing operational contexts while maintaining probabilistic coherence, computational efficiency, and theoretical guarantees. This limitation manifests in multiple ways across the reviewed literature.
First, graphical model structures, whether functional decompositions (Kapteyn et al., 2021) or event-based partitions (Zhao et al., 2024), are specified a priori based on engineering judgment and remain fixed during operation. The conditional independence assumptions that enable computational tractability reflect design-time expectations about system behaviour, not observed statistical dependencies during deployment. When operational context changes (sensors degrade, adversarial actions modify environmental conditions, or even faults alter system dynamics) the specified independence assumptions may no longer hold, compromising both computational efficiency (if independent modules must now communicate frequently) and accuracy (if unmodeled dependencies lead to biased predictions).
Second, information-passing mechanisms assume fixed message-passing protocols that do not adapt to observed data. Autoregressive structures (Kennedy & O'Hagan, 2000) impose predetermined orderings, while GNN architectures (Taghizadeh et al., 2024) employ fixed graph topologies specified before training. Neither approach provides mechanisms for online learning of message-passing patterns based on streaming observations. When statistical dependencies shift (as they inevitably do in contested, dynamic environments) fixed information-passing protocols continue executing the same operations, propagating information along channels that may no longer be relevant while neglecting newly important dependencies.
Third, in the cavity of computational approximations, there exist several potential solutions like variational inference (Salimbeni & Deisenroth, 2017), multi-fidelity modeling (Peherstorfer et al., 2018), sparse inducing points (Hensman et al., 2013); however, these too make fixed trade-offs between accuracy and efficiency that do not adapt to changing requirements. During nominal operations with ample computational resources, conservative approximations sacrifice unnecessary computational cost for marginal accuracy improvements. During time-critical situations requiring rapid decisions, aggressive approximations trade accuracy for speed. Current frameworks lack mechanisms for dynamically adjusting approximation fidelity based on available computational resources and decision urgency.
Fourth, uncertainty quantification methods provide no theoretical guarantees during regime transitions. Interval methods (Zhao et al., 2024) guarantee coverage assuming module models remain valid, but offer no guidance when model adequacy is uncertain. Variational inference (Blei et al., 2017) provides lower bounds on marginal likelihoods for model comparison, but these bounds depend on the variational family specification and may become uninformative precisely when model selection is most critical. Moreover, as a passing remarks, the literature provides limited tools for quantifying uncertainty about uncertainty estimates, meta-uncertainty that reflects epistemic limitations in model specification and approximation quality.
These interconnected limitations point toward a clear research opportunity: adaptive Bayesian network architectures that dynamically reconfigure module dependencies, information-passing protocols, and approximation strategies based on operational context, while maintaining probabilistic coherence and providing bounded uncertainty during transitions. Such architectures would enable autonomous systems to maintain accurate uncertainty quantification across regime changes without requiring human intervention to redesign graphical model structures.
Conclusions and Future Directions
This review has identified a critical limitation in current modular Bayesian frameworks for digital twins: the reliance on static architectures that cannot adapt to evolving operational contexts whilst maintaining probabilistic coherence. Although probabilistic graphical models (Kapteyn et al., 2021), multi-fidelity modelling frameworks (Zhang & Alemazkoor, 2024), and Bayesian verification methods (Zhao et al., 2024) have established rigorous foundations for uncertainty quantification in decomposed systems, these approaches uniformly assume fixed module dependencies, predetermined information-passing protocols, and non-adaptive computational approximations. For autonomous systems operating in contested environments, where adversarial actions, sensor degradation, and fault conditions fundamentally alter statistical dependencies, this assumption proves untenable. The central tension between computational tractability and rigorous uncertainty quantification remains unresolved. Current methods achieve real-time performance by specifying conditional independence structures at design time that may not reflect runtime statistical dependencies. When operational regimes shift (precisely when accurate uncertainty quantification is most critical) fixed architectures propagate information along obsolete channels whilst neglecting newly emergent correlations.
Three interconnected research directions emerge: adaptive graphical model structures that dynamically reconfigure based on observed data, context-aware information-passing protocols that balance sparse efficiency against dense accuracy, and dynamic approximation strategies that adjust fidelity based on computational resources and decision urgency. These capabilities are essential for autonomous operations in denied, degraded, and operationally limited environments, where human intervention may be infeasible. Future work should prioritise empirical validation on physical systems under realistic contested scenarios, moving beyond simulated environments to establish whether adaptive frameworks deliver on their theoretical promise.
References
Bishop, P., Bloomfield, R., & Cyra, L. (2011) 'Combining testing and proof to gain high assurance in software: A case study', in Proceedings of SAFECOMP 2011, Springer, pp. 206-219.
Blei, D. M., Kucukelbir, A., & McAuliffe, J. D. (2017) 'Variational inference: A review for statisticians', Journal of the American Statistical Association, 112(518), pp. 859-877.
Češka, M., Dannenberg, F., Paoletti, N., Kwiatkowska, M., & Brim, L. (2016) 'Precise parameter synthesis for stochastic biochemical systems', Acta Informatica, 54(6), pp. 589-623.
Chen, Y. P., He, W., Jiang, Z., Xiao, T., Xu, Z., & Li, Y. (2025) 'Uncertainty-aware digital twins: Robust model predictive control using time-series deep quantile learning', arXiv preprint arXiv:2501.10337.
Darema, F. (2004) 'Dynamic data driven applications systems: A new paradigm for application simulations and measurements', in Computational Science—ICCS 2004, Springer, pp. 662-669.
Das, A., Kong, W., Leach, A., Mathur, S., Sen, R., & Yu, R. (2023) 'Long-term forecasting with TiDE: Time-series dense encoder', arXiv preprint arXiv:2304.08424.
Defence and Security Accelerator (DSTL) (2022) 'Digital Twin Official Definition'. Available at: https://www.gov.uk/government/publications/digital-twin-definition/digital-twin-official (Accessed: 23 November 2025).
Fan, C., Zhang, Y., Pan, Y., Li, X., Zhang, C., Yuan, R., Wu, D., Wang, W., Pei, J., & Huang, H. (2020) 'Multi-horizon time series forecasting with temporal attention learning', in Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, pp. 2527-2535.
Hensman, J., Fusi, N., & Lawrence, N. D. (2013) 'Gaussian processes for big data', in Proceedings of the 29th Conference on Uncertainty in Artificial Intelligence, pp. 282-290.
Kapteyn, M. G., Pretorius, J. V., & Willcox, K. E. (2021) 'A probabilistic graphical model foundation for enabling predictive digital twins at scale', Nature Computational Science, 1(5), pp. 337-347.
Kennedy, M. C., & O'Hagan, A. (2000) 'Predicting the output from a complex computer code when fast approximations are available', Biometrika, 87(1), pp. 1-13.
Kennedy, M. C., & O'Hagan, A. (2001) 'Bayesian calibration of computer models', Journal of the Royal Statistical Society: Series B, 63(3), pp. 425-464.
Koller, D., & Friedman, N. (2009) Probabilistic graphical models: Principles and techniques. MIT Press.
Kyzyurova, K. N., Berger, J. O., & Wolpert, R. L. (2018) 'Coupling computer models through linking their statistical emulators', SIAM/ASA Journal on Uncertainty Quantification, 6(3), pp. 1151-1171.
Mayne, D. Q., Rawlings, J. B., Rao, C. V., & Scokaert, P. O. (2000) 'Constrained model predictive control: Stability and optimality', Automatica, 36(6), pp. 789-814.
Ming, D., & Guillas, S. (2021) 'Linked Gaussian process emulation for systems of computer models using Matérn kernels and adaptive design', SIAM/ASA Journal on Uncertainty Quantification, 9(4), pp. 1615-1642.
Ming, D., Williamson, D., & Guillas, S. (2023) 'Deep Gaussian process emulation using stochastic imputation', Technometrics, 65(2), pp. 150-161.
Peherstorfer, B., Willcox, K., & Gunzburger, M. (2018) 'Survey of multifidelity methods in uncertainty propagation, inference, and optimization', SIAM Review, 60(3), pp. 550-591.
Rawlings, J. B., & Mayne, D. Q. (2009) Model predictive control: Theory and design. Nob Hill Publishing.
Russell, S. J., & Norvig, P. (2002) Artificial intelligence: A modern approach (2nd ed.). Pearson.
Salimbeni, H., & Deisenroth, M. (2017) 'Doubly stochastic variational inference for deep Gaussian processes', in Advances in Neural Information Processing Systems, Vol. 30, pp. 4588-4599.
Sauer, A., Gramacy, R. B., & Higdon, D. (2022) 'Active learning for deep Gaussian process surrogates', Technometrics, 65(1), pp. 4-18.
Strigini, L., & Povyakalo, A. (2013) 'Software fault-freeness and reliability predictions', in Proceedings of SAFECOMP 2013, Springer, pp. 106-117.
Taghizadeh, S., Karimi, A., & Heitzinger, C. (2024) 'Hierarchical multi-fidelity graph neural networks for solving partial differential equations', Journal of Computational Physics, 485, 112102.
Volodina, V., Cancelo, J. R., & Dent, C. J. (2022) 'Propagating uncertainty in power system dynamic simulations using polynomial chaos', in Proceedings of the 2022 17th International Conference on Probabilistic Methods Applied to Power Systems, IEEE, pp. 1-6.
Walter, G., & Augustin, T. (2009) 'Imprecision and prior-data conflict in generalized Bayesian inference', Journal of Statistical Theory and Practice, 3(1), pp. 255-271.
Walter, G., Graham, A., & Augustin, T. (2017) 'Bayesian inference and uncertainty quantification under strong prior-data conflict', in Soft Methods for Data Science, Springer, pp. 495-502.
Wilson, A. L., Dent, C. J., & Goldstein, M. (2018) 'Quantifying uncertainty in energy forecasts from offshore wind farms', Energy Procedia, 137, pp. 42-55.
Zhang, R., & Alemazkoor, N. (2024) 'Multi-fidelity machine learning for uncertainty quantification and optimization', Journal of Machine Learning for Modeling and Computing, 5(4), pp. 77-94.
Zhao, X., Delicaris, J., Oswald, N., Schmid, S., Calinescu, R., Cavalcanti, A., & Woodcock, J. (2024) 'Bayesian learning for the robust verification of autonomous robots', Communications Engineering, 3(1), 24.